Hierarchical deterministic wallets protect you from losing your bitcoins (or colored coins) accidentally: by storing encrypted backups of the single root of your wallet tree, you can later gain control of all the coins that you've ever received. See for example this short presentation.
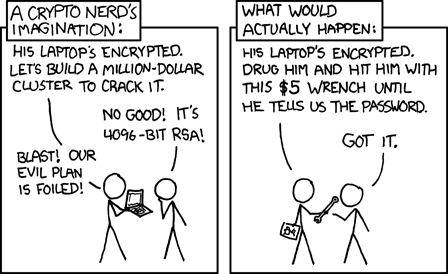
However, there are other dangers beside accidental loss of your secret data. In particular, how will you protect yourself from a robber who threatens to harm you unless you decrypt your wallet file to let him steal your coins? The famous xkcd 538 cartoon describes a similar circumstance:
By using an hierarchical deterministic wallet, you can have a "hot" sub-tree where you maintain only a few coins for your daily transactions, so if for example the robber sees the wallet balance on your screen he will think that those are the only coins that you got. After you decrypt this sub-tree for the robber, the vast majority of your coins will remain safe.
Still, as we will see next, a savvy robber may examine the total size of your encrypted wallet data, infer that your hot sub-tree is a decoy, and try to force you to also decrypt your "cold" storage. Of course, to protect in advance against this scenario you can resort to the simple option of having a separate wallet file for cold storage, with the hope that the robber will be unaware of the separate file. But if you access your separate cold wallet with some frequency, you'll need to have a procedure to fetch and decrypt the cold wallet, so the robber may scan your other files or look for instructions that you prepared regarding cold storage access. For most people, keeping the cold storage as a totally obscure file that looks like junk is very risky, because they might delete it or forget how to use it.
Therefore, it is preferable to have an orderly solution that is safe for common people.
Users of encryption software such as TrueCrypt are probably familiar with the deniable encryption capability that enables having a decoy partition. The problem with it, as with the hot/cold wallet issue, is that the robber can see that the total amount of encrypted data is larger than the partition that you decrypted for him.
Maybe it is always possible to create a ciphertext with a decoy that is indistinguishable from a ciphertext without a decoy? Unfortunately, this cannot be done. Since it is simple enough to prove that it's impossible, let us provide a rigorous proof here (refer also to section 5 of this paper). As described in a bitcointalk post, the problem stems from the fact that symmetric encryption is highly efficient: the size of the encrypted data is the same as the size of the plain data. Suppose that you have two incompressible files f1 and f2 (i.e., files with high entropy) of same size. It is possible to encrypt f1 into a ciphertext c such that the sizes of f1 and c are the same. If you could create a ciphertext c0 of same size as f1 that can be decrypted into f1 by using the secret key k1 and can be decrypted into f2 by using another secret key k2, then you effectively compressed (f1,f2) into (c0,k1,k2). This is impossible because the key sizes do not depend on the file sizes but rather on a security parameter, for example you can use a 128-bit key to encrypt files of any size so that the encryption is unbreakable in less than ≈2^128 iterations. Therefore, we deduce that c0 must be larger than c, which completes the proof.
So the robber can distinguish between a user who creates both a decoy wallet hierarchy and a real wallet hierarchy, versus a user who creates only a real wallet hierarchy, because the encrypted data size of the first user will be larger.
To overcome this problem in a way that works well for ordinary people, my bitcointalk post above suggests the technique of encrypting junk data in popular wallet clients by default, so that even users who don't care about deniable encryption will have a wallet file that looks the same as wallets that do contain a decoy. Since the wallet data is just a collection of secret keys, what we're talking about here are small files of few dozens of kilobytes usually, so doubling the size is not much of a burden.
To protect against scenarios where the robber has a reason to suspect that the user did use deniable encryption, and therefore try to force the user to decrypt his decoy wallet, it might be preferable to concatenate some n<N ciphertexts of variable sizes, instead of two ciphertexts of equal size, where n is random and N is some fixed bound. This way, the attacker wouldn't even know how many decoy wallets are contained in the ciphertext.
Could there be even better ways to implement this kind of protection? Probably not. One suggestion is to store in your encrypted wallet file only master secret keys for root nodes of the hierarchical deterministic wallet, thereby not giving the robber any hints regarding what you're actually storing, as those secret keys are of a very small fixed size. However, you'll then need to re-scan your entire tree hierarchy every time that you view your wallet, e.g., to see if you received payments. In case the robber attacks you during the re-scan procedure, you'd be vulnerable. This is highly risky because the re-scan procedure is quite demanding, you cannot even be completely sure when to terminate the procedure because payments aren't necessarily in consecutive derived nodes (discussed for example at this bitcointalk post), and this uncertainty becomes aggravated in case the topology of your tree hierarchy is nonstandard. To add to that, if you wish to parse only the UTXO set instead of the entire blockchain from genesis, then you won't be able to list your transactions history (e.g., if you sent 20 BTC to Alice's address a month ago then you won't see that), and commonly people wouldn't want to lose this transactions history feature as they would otherwise can easily become confused regarding the status of their current balance. Therefore, this suggestion is inferior to storing the entire tree hierarchy of your wallet on disk with deniable encryption, so that you can type your real password and instantly gain access to your full wallet (and update it quickly in case your Bitcoin client already fetched the latest blocks), and then re-encrypt and thereby make your wallet instantly disappear without storing evidence that it ever existed. Moreover, an important objective is to protect people who aren't technically savvy, and requiring the re-scan procedure for normal usage is a bad idea because people would just leave their wallets loaded all the time in decrypted form, to avoid being bothered (similarly to people who attach sticky notes with passwords to their office computer screen because they've been asked to remember multiple passwords).
In addition to security against robbers, Bitcoin wallets with deniable encryption can also provide plausible deniability in the legal sense. For example, people who wish to gamble in places where it's unlawful, or make donations to illicit organizations, may prefer to conduct their financial activity under a deniable encryption layer.